로또에 대한 잘못된 상식
경제학 | 2006/05/27 22:57
"로또에 당첨된 확률은?" 이라는 질문을 들어 본경우는 많을 것이다.
그리고 대부분의 사람들은 약 800만 분의 1정도의 확률 이라는 것을 들어본 경험이 있을것이다.
이걸 "벼락 16번 맞을 확률이다." 라는 둥의 이야기가 돌아다니는데 이게 과연 맞는 소리일까?
이 의문을 해결하기 위하여 떠나보자
우선 벼락 16번 맞는 확률이라는 이야기의 시작은 어디인가?
인터넷의 과거 신문 기사를 검색해본 결과 두가지의 기사를 찾을수 있었다.
[로또와 인쇄복권 수학적 확률] “벼락 16번 맞기보다 어렵다” [국민일보 2003-02-12 15:46]
http://news.naver.com/news/read.php?mode=LSD&office_id=005&article_id=0000137291§ion_id=105&menu_id=105
[정의구현 사전] 로또[loto] n. 英 lotto.[한겨레21 2005-10-11 09:09]
http://news.naver.com/news/read.php?mode=LSD&office_id=036&article_id=0000009702§ion_id=102&menu_id=102
어디에도 이 벼락 맞을 확률수치가 어느 데이터로 부터 유래했다는 내용은 없다.
그러나 데이터가 통계데이터로 부터 유래했다고 해도
이 확률은 문제가 있다고 본다. 표본집단이 어디냐에 대한 문제이다.
도시에 사는 사람이 벼락 맞을 확률은 얼마일까? 50만분에 1?
절대 아니다.
도시의 건물들마다 꼭대기에 가느다란 꼬챙이가 보일것이다... 피!뢰!침!
피뢰침이 있는 건물 주변부에서 벼락맞을 확률은 0에 가깝다.
아마도 저 50만분에 1이라는 확률은 비오는날 들판을 가다가 벼락 맞을 확률일 것이다.
당연히 우리나라 처럼 도시화가 진행된 나라에서는 주위에 벼락맞아 죽는 사람을 볼 수 없는것이다.
게다가 비오는날 벼락 맞으려고 들판에 나가 서 있는 사람이 있는가? 없다.
당연히 회피하려하므로 확률은 극도로 감소한다.
벼락맞을 확률이라는건 그 어감이 주는 느낌을 살리는 거지 정말 벼락 맞을 확률은 아니라는 거다.
그 다음으로 1/8145060 이라는 확률
이게 내가 로또 1등에 당첨될 확률이라는 건 분명하다.
하지만 통계학을 수강해보신분이라면 이게 누군가가 로또에 당첨되는 확률은 아니라는 것을 금방 발견할것이다.
이에 관한 일화로 미국에서 유의 할만한 사건이 있었다.
1964년 LA에서 꽁지머리의 금발 소녀가 한 여성의 지갑을 훔쳐 콧수염과 턱수염을 기른 흑인 남자가 운전하는 노랑색 자동차를 타고 도주하는 사건이 발생하였다. 경찰은 노랑색 자동차를 가진 콧수염과 턱수염을 기른 흑인 남자를 잘 아는 금발 꽁지머리 여자 Janet Collins라는 여자를 체포하였다. 당시 사건의 물증은 없었다. 검사는 다음과 같은 통계 확률과 정황 증거로 Collins의 유죄를 주장했다.
이 확률을 모두 곱해서 이러한 특징을 가진 커플이 존재할확률은 무려 1/12000000 (천이백만분의 일)
로또 확률 보다 더 낮은 수치이다. 당연히 유죄로 보이는가?
당시 배심원들에게 이 주장은 받아 들여져서 2급 절도죄의 평결을 받았다.
그러나 여기서 끝이 아니다. 당연히 Collins는 항소했고 캘리포니아주 대법원은 Collins의 변호사 주장을 받아들여
이 판결이 애매한 통계적 확률에 의존하고 있다면서 고등법원으로 사건을 돌려보냈다.
그럼 Collins의 변호사 주장은 무엇이었을까?
Ms. Collins의 변호인은 사건의 확률을 다른 시각에서 볼 것을 주장하였다.
주위에 있을 수 있으면서 절도 가능성이 있는 couple의 숫자를 n
한 couple이 6가지 특성을 만족할 확률을 p라고 하자
X 를 이 조건을 만족하는 couple 숫자를 나타내는 확률변수라고 하면 이 경우 X가 이항분포(결과가 0,1둘뿐)를 따른다는 것은 이론의 여지가 없으므로
(위의 식은 일반 계산기로는 유효한 숫자범위 문제로 표의 값을 계산할수 없고 수학용 프로그램을 사용해야 한다.)
그렇다면 이 경우 n을변화시킨다면...
확률은 다음과 같이 변화한다.
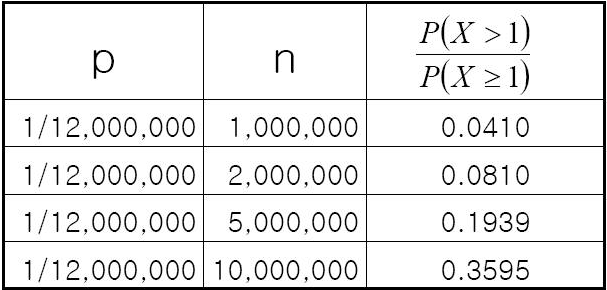
천 이백만분의 일의 확률인데도 "누군가가" 존재할 확률은 터무니 없이 상승해버린다.
로또의 경우는 이보다 더 높을 것이다.
(위의 식은 일반 계산기로는 유효한 숫자범위 문제로 표의 값을 계산할수 없고 수학용 프로그램을 사용해야 한다. 본인은 그런 프로그램을 보유하지 못해서 로또에 대해서는 직접 계산해볼수 없다.)
이것이 1/8145060 이 나에게만 유효하지 로또구입자 전체에게 유효하지 않은 이유이다.
따라서 한주에 너댓명 나오는게 이상할게 하나도 없는 .....
그리고 대부분의 사람들은 약 800만 분의 1정도의 확률 이라는 것을 들어본 경험이 있을것이다.
이걸 "벼락 16번 맞을 확률이다." 라는 둥의 이야기가 돌아다니는데 이게 과연 맞는 소리일까?
이 의문을 해결하기 위하여 떠나보자
우선 벼락 16번 맞는 확률이라는 이야기의 시작은 어디인가?
인터넷의 과거 신문 기사를 검색해본 결과 두가지의 기사를 찾을수 있었다.
[로또와 인쇄복권 수학적 확률] “벼락 16번 맞기보다 어렵다” [국민일보 2003-02-12 15:46]
http://news.naver.com/news/read.php?mode=LSD&office_id=005&article_id=0000137291§ion_id=105&menu_id=105
[정의구현 사전] 로또[loto] n. 英 lotto.[한겨레21 2005-10-11 09:09]
http://news.naver.com/news/read.php?mode=LSD&office_id=036&article_id=0000009702§ion_id=102&menu_id=102
어디에도 이 벼락 맞을 확률수치가 어느 데이터로 부터 유래했다는 내용은 없다.
그러나 데이터가 통계데이터로 부터 유래했다고 해도
이 확률은 문제가 있다고 본다. 표본집단이 어디냐에 대한 문제이다.
도시에 사는 사람이 벼락 맞을 확률은 얼마일까? 50만분에 1?
절대 아니다.
도시의 건물들마다 꼭대기에 가느다란 꼬챙이가 보일것이다... 피!뢰!침!
피뢰침이 있는 건물 주변부에서 벼락맞을 확률은 0에 가깝다.
아마도 저 50만분에 1이라는 확률은 비오는날 들판을 가다가 벼락 맞을 확률일 것이다.
당연히 우리나라 처럼 도시화가 진행된 나라에서는 주위에 벼락맞아 죽는 사람을 볼 수 없는것이다.
게다가 비오는날 벼락 맞으려고 들판에 나가 서 있는 사람이 있는가? 없다.
당연히 회피하려하므로 확률은 극도로 감소한다.
벼락맞을 확률이라는건 그 어감이 주는 느낌을 살리는 거지 정말 벼락 맞을 확률은 아니라는 거다.
그 다음으로 1/8145060 이라는 확률
이게 내가 로또 1등에 당첨될 확률이라는 건 분명하다.
하지만 통계학을 수강해보신분이라면 이게 누군가가 로또에 당첨되는 확률은 아니라는 것을 금방 발견할것이다.
이에 관한 일화로 미국에서 유의 할만한 사건이 있었다.
1964년 LA에서 꽁지머리의 금발 소녀가 한 여성의 지갑을 훔쳐 콧수염과 턱수염을 기른 흑인 남자가 운전하는 노랑색 자동차를 타고 도주하는 사건이 발생하였다. 경찰은 노랑색 자동차를 가진 콧수염과 턱수염을 기른 흑인 남자를 잘 아는 금발 꽁지머리 여자 Janet Collins라는 여자를 체포하였다. 당시 사건의 물증은 없었다. 검사는 다음과 같은 통계 확률과 정황 증거로 Collins의 유죄를 주장했다.
차를 타고 다니는 다른 인종 couple 1/1000
턱수염을 한 흑인 1/10
금발 여자 1/3
꽁지머리 여자 1/10
콧수염 남자 1/4
노란색 자동차 1/10
턱수염을 한 흑인 1/10
금발 여자 1/3
꽁지머리 여자 1/10
콧수염 남자 1/4
노란색 자동차 1/10
이 확률을 모두 곱해서 이러한 특징을 가진 커플이 존재할확률은 무려 1/12000000 (천이백만분의 일)
로또 확률 보다 더 낮은 수치이다. 당연히 유죄로 보이는가?
당시 배심원들에게 이 주장은 받아 들여져서 2급 절도죄의 평결을 받았다.
그러나 여기서 끝이 아니다. 당연히 Collins는 항소했고 캘리포니아주 대법원은 Collins의 변호사 주장을 받아들여
이 판결이 애매한 통계적 확률에 의존하고 있다면서 고등법원으로 사건을 돌려보냈다.
그럼 Collins의 변호사 주장은 무엇이었을까?
Ms. Collins의 변호인은 사건의 확률을 다른 시각에서 볼 것을 주장하였다.
주위에 있을 수 있으면서 절도 가능성이 있는 couple의 숫자를 n
한 couple이 6가지 특성을 만족할 확률을 p라고 하자
X 를 이 조건을 만족하는 couple 숫자를 나타내는 확률변수라고 하면 이 경우 X가 이항분포(결과가 0,1둘뿐)를 따른다는 것은 이론의 여지가 없으므로
(위의 식은 일반 계산기로는 유효한 숫자범위 문제로 표의 값을 계산할수 없고 수학용 프로그램을 사용해야 한다.)
그렇다면 이 경우 n을변화시킨다면...
확률은 다음과 같이 변화한다.
천 이백만분의 일의 확률인데도 "누군가가" 존재할 확률은 터무니 없이 상승해버린다.
로또의 경우는 이보다 더 높을 것이다.
(위의 식은 일반 계산기로는 유효한 숫자범위 문제로 표의 값을 계산할수 없고 수학용 프로그램을 사용해야 한다. 본인은 그런 프로그램을 보유하지 못해서 로또에 대해서는 직접 계산해볼수 없다.)
이것이 1/8145060 이 나에게만 유효하지 로또구입자 전체에게 유효하지 않은 이유이다.
따라서 한주에 너댓명 나오는게 이상할게 하나도 없는 .....
trackback :: http://engagestory.com/trackback/67
웹에서 계산하면 되지 않나요? 구글이나....
안됩니다. 똑같이 오류나서 전용 프로그램을 사용해야 됩니다.
계산하는데 꽤 시간이 걸려요